Please note this is a page storing my preparation for the exam, I have just sat the exam but as yet do not know if I passed… (Update – I passed so take that for what it’s worth…)

For actual expert advice this course is highly recommended from people I know who’ve done it.

The critical appraisal exam is probably the earliest part of the exam you’ll sit. It follows a clear format and if you manage to get access to some old papers you’ll see some recurring themes and questions. I have been repeatedly told that doing practice papers under exam conditions (time yourself, sit at a desk, use the pencil you will use…) is one of the most useful things you can do. Apparently you have to write in pencil for the exam which was news to me but this may be something you need to take into consideration.

The first place to start is the College website.

• FRCEM Page
• advice on prep and common errors [pdf]
• most frequently offered answers [pdf]

St Emlyns have a number of great resources worth checking out

• Main Post on general tips for the exam
• Podcast one and two on stats
• Intro to Power Calculations
• Journal Club
• SMACC Gold Research Workshop
• The StEmlyns Critical Appraisal Nuggets (CANS) podcasy with Rick and Simon

RCEM Learning has several modules on critical appraisal from Adrian Boyle. These have the advantages of having questions that you can test yourself on.

• Specificity
• Sensitivity
• Receiver Operating Curves
• Relative Risk
• Positive Predictive Values
• Number Needed to Harm
• Likelihood ratio of a positive test
• Likelihood ratio of a negative test
• Negative Predictive Value
• Number Needed to treat
• Accuracy
• Absolute risk reduction
• How to appraise
  • a treatment
    • EDGT
    • hand lacerations
  • a Systematic review
  • a diagnostic test – d dimer

Not exam specific but damn good…:

• EM Lit of Note
• EM Nerd
• The Bottom Line
• How to read a paper – a good old style book but still a classic

Remember there’s a limited range of study types that you’re likely to be asked to be about:

• Diagnostic studies
• Therapeutic studies
• Meta-analysis

Writing the abstract

This is one of the key parts of the exam. Generally it is 200 words to summarise (not rewrite) the paper. You need to practice this so you have an idea of what 200 of your words under exam conditions actually looks like on a physical piece of paper.

Use some kind of structured approach

• IMRAD
  • Introduction (aim)
  • Methods
  • Results
  • And Discussion
• PICO
  • Population
  • Intervention
  • Comparison
  • Outcome

Ken Milne over at the SGEM has published the BEEM tools for critical appraisal of different types of studies that can be freely downloaded here

• BEEM Tool RCT
• BEEM Tool Diagnostic study

In a diagnostic paper you’ll need to identify:

• the index test – the test under investigation
• the reference standard – the gold standard that defines whether or not the patient has the disease
• the target diagnosis – what where they looking to diagnose? Acute MI, SAH etc…

Remember to mention what type of study it is eg a randomised control trial or observational study

Definitions for the exam:

Methods Section

Type I Error [false positive][sometimes called alpha error]

•  A type I error is said to have occurred when we reject the null hypothesis incorrectly (i.e. the null hypothesis is true and there is no difference between the two groups) and report a difference between the two groups being studied. Typically when numbers are small and you find a +ve result by chance or by multiple testing

Type II Error [false negative][sometimes called beta error]

•  A type II error is said to occur when we accept the null hypothesis incorrectly (i.e. it is false and there is a difference between the two groups which is the alternative hypothesis) and report that there is no difference between the two groups. Typically when numbers are small and you find a negative result.
  • look for wide CIs (suggests imprecision)
  • look at the extreme ends of the CIs – is an important, clinically meaningful difference included?
  • look at the power calc – was the alpha and beta appropriate – should they have been more realistic about the difference they should have looked for.
• Both type I and type II errors are conceptual and you cannot tell if they have occurred. You can only talk about the potential for type I and II errors

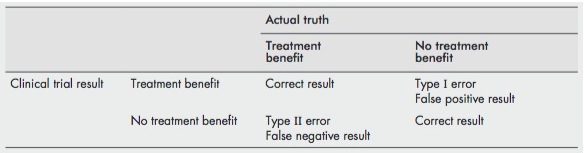[ref]

This is a great image describing the difference between a type I and II error:

• “power” refers to the number of patients required to avoid a type II error in a comparative study [ref]
• “Power is the probability of observing the smallest effect of clinical interest, if it exists in the population.” [ref]
• The power of a study is defined as 1 – beta
• Power is determined by
  • 1. the level at which alpha is set;
  • 2. the sample size; [useful St Emlyms Podcast]
  • 3. the variability of the outcome measure, as defined by its standard deviation
  • 4. the minimum clinically significant difference we wish to detect. Investigators must decide this
• By convention the risk of type I error should be minimised if p<0.05 (which is why that comes up all time) and the type II error should be minimised if p<0.2 (that’s why they always talk about 80% chance of finding a specific difference). Note that the tendency therefore will be more likely to have a type II than a type I error
• note you can (and probably should) perform a power calculation for diagnostic studies as well as comparative studies. In this case the minimally clinically significant difference should be substituted for adequate sensitivity or specificity.[ref]

Alpha: The level at which statistical significance is set is called alpha [conventionally <0.05]

Beta: the probability of a false negative result, as determined by the sample size. [conventionally <0.2]

Non-inferiority trial

• FOAMed paper here and BMJ here
• These are not equivalence trials, though people have used the terms equivalence and non inferiority interchangeable. Bioequivalence trials of drugs are probably the only true equivalence trials
• You must specify a noninferiority margin – for it to be a positive trial the primary outcome has to be within a certain margin of the existing treatment. Selection of this margin is unavoidably subjective and is open to all kinds of fudging.
• These trials are suitable when you are testing something that you assume will be at best non inferior. For example face to face versus telephone consultation – no one expects telephone to be better but it might be non inferior. So instead of assuming the null hypothesis (that there is no difference between treatments – this is what we normally assume in superiority trials) and trying to disprove it; in a non inferiority trial the null hypothesis is that the new intervention is not as good and you are trying to prove that is non inferior.
• Of note, blinding is much less use in a non inferiority trial as a biased but still blinded end point assessor can just give everyone equivalent outcomes and the new drug being assessed comes out as non inferior.
• ‘intention to treat’ and ‘per protocol’ analyses can both bias the results. Typically ITT is the way to go but in non inferiority trials you typically need both ITT and per protocol analyses to be positive for the intervention to be truly non inferior.
• non inferior trials are typically analysed on a confidence interval but without the p value. This is in the Sedgwick paper but I still struggle to understand why they don’t use the p value.

Intention to treat

•  intention-to-treat analysis means that patients are analysed in the group to which they were originally randomised, regardless of whether they actually received the treatment they were allocated to. It ensures that the protection from bias created by allocation concealment is maintained. The downside is that the estimate of effect is likely on the conservative side

 What is a hypothesis

• A hypothesis is a prediction, should be supported by theory. In other words, there should be a clear explanation of why we might expect the hypothesis to be true
• Hypothesis testing is typically with p values whereas estimation is typcially with confidence intervals.
• Hypothesis testing should require the researcher to decide before the study starts what difference is considered to be clinically significant

Pragmatic Research: Pragmatic research simply asks whether a treatment works, or how useful a test is, in routine practice. It does not attempt to determine whether the treatment could work under certain circumstances or try to determine how or why a treatment works.

Explanatory Research: Explanatory research explores how or why a treatment works or whether it works under specific (usually ideal) circumstances.

Systematic Review

1.  literature searching and retrieval
2. the selection of appropriate papers
3. quality assessment of selected papers.

Different from narrative review

• possible to apply statistical techniques to the data
• predefined criteria for quality of data
• explicit methods with comprehensive search
• focussed question

• Quality assessment should be objective (Jadad does this) the key factors are:
  • lack of allocation concealment,
  • lack of blinding,
  • inadequate follow-up
  • failure to use intention-to-treat analysis.
• assessing heterogeneity in systematic reviews
  • two ways
    • look at the forest plot, if they’re all no where near each other then heterogeneity is present
    • apply statistical tests, typically a significant result implies heterogeneity (the tpa meta analysis a good example of that)
• There are established guidelines for doing and reporting systematic reviews, PRISMA and the Cochrane handbook are two good sources and it’s worth checking to see if the authors have done this.

Meta Analysis

• assumes that all the individual studies are estimates of the same value
• designed as a way of reducing type II error (ie not finding an effect when it is there – the steroids in headache papers are a good example)
• Goodacre suggests that simply looking at the studies individually to see what they were measuring is a good way to look for heterogeneity
• Great quote “However, it may become apparent that the statisticians, for all their fancy tests, are not just trying to combine apples and oranges. They are trying to combine apples, oranges, potatoes and cabbages, with the odd sock thrown in as well” [ref]

Publication bias

• Publication bias occurs when the results of a study influence the likelihood that it will be written up

What is a crossover trial?

• patients act as their own control.
• typically one treatment followed by a wash out period followed by the next treatment
• Can be placebo and blinded
• fewer patients are needed

Placebo controlled trials

• Specifically, placebos should not be used unless no proved intervention exists, or there are compelling and scientifically sound reasons why a placebo should be used to determine the efficacy or safety of an intervention [from declaration of helsinki 2008] the idea being that it’s very easy to prove superiority against placebo and much more difficult in trialling it against the best current evidence

Randomisation:

• “Randomisation is a technique used to ensure that allocation to treatment group is not influenced by carers, patients or researchers.” [ref]
• the main problem comes if people are able to predict which group people end up in – best example is that of alternate week days.
• cluster randomisation can be used to randomise groups of patients rather than individuals. Though remember this usually ruins allocation concealment. An example would be different hospitals randomised to different treatments.
  • Advantages
    •  Overcomes bias associated with non- randomised methods
    • Reduces “contamination” that may occur in individual patient randomisation
    • May be feasible when individual randomisation is not
  • Disadvantages
    • Allocation concealment not usually possible
    • Patients, carers or researchers may choose when or where to access their desired service
    • Patients may choose whether to enter the trial depending upon what service is available
    • Standard statistical tests are not appropriate
    • Need to take clustering of data into account
    • Statistical power may be substantially reduced
• block randomisation
  • block randomisation is used to allocate participants to treatment to ensure similar numbers of participants in the groups
  • within the block the sequence is defined (e.g. in a block of 4 in 1:1 ration, 2 would be placebo, 2 would be active, the order would still be randomised within the block)
  • ensures similar patient numbers in each group in small trials. In large trials not really needed as probability will even things out
  • small block sizes can be predicted if there is no blinding therefore ruining allocation concealment

• stratified randomisation
  • used to ensure that equal numbers of participants with a characteristic thought to affect prognosis or response to the intervention will be allocated to each comparison group. eg stratified by severity of disease.
  • i think of it as similar to block randomisation but instead of ensuring the numbers in each group are equal it ensures the proportions of patients with a certain characteristic (eg smoking status) are similar between the two groups.

Allocation concealment

• this is to prevent withdrawal once someone finds out they’re in placebo. It ensures there is no bias in allocation.
• it is NOT the same as blinding
• “A technique used to prevent selection bias by concealing the allocation sequence from those assigning participants to intervention groups, until the moment of assignment. Allocation concealment prevents researchers from (unconsciously or otherwise) influencing which participants are assigned to a given intervention group.” [ref]
• best method is central telephone: all patient data is given to the trial prior to allocation
• consecutive sealed envelopes will also allow this but are open to compromise (opening the envelope early, holding it to the light etc…)
• block randomisation is only appropriate if allocation concealment is working.
• allocation bias is the systematic difference between participants in how they are allocated to treatment.

Blinding

• this occurs following randomisation – as opposed to allocation concealment which occurs prior to randomisation.
• blinding is designed to ensure measuring of outcomes is free from bias

Reference Standard:

• The reference standard is the criterion by which it is decided that the patient has, or does not have, the disease.
• An ideal reference standard should correctly classify patients with and without disease.
• Ideally all patients should get the reference standard
• the diagnostic test being evaluated should not be part of the reference standard. [incorporation bias] [this overestimates specificity]
• When the diagnostic test under evaluation determines what reference standard is used then it is work up bias. [This overestimates sensitivity]
• The person measuring or interpreting the diagnostic test under evaluation should be blinded to the results of the reference standard. Likewise, the person measuring or interpreting the reference standard should be blinded to the results of the diagnostic test under evaluation

For trials of service delivery some points worth thinking about:

• Randomised v non-randomised studies
• Cluster (group) randomisation
• Historical v contemporaneous controls
• The Hawthorne Effect
• Sustainability
• Generalisability

Sampling methods

• Convenience sample
  • subjects are recruited into the trial at the convenience of the investigators – the most common reason being research assistant availability. This is open to selection bias as it’s possible that subjects presenting outside the times of research assistant availability are systematically different from those presenting during “office hours” [ref]
• Random sampling
  • not especially relevant to EM but involves having a list of all people with a certain disease (say for example a cancer registry) and selecting at random  from that list. [ref]
• Consecutive sampling
  • this is probably ideal for EM studies as we want to capture all the patients with the disease of interest presenting to our EDs. This gives the best representation of patients for either therapeutic studies or diagnostic studies. [ref]

Statistical tests 

• Mann Whitney U Test: used to compare continuous (or ordinal) data in two independent groups, when the data is non parametric or skewed (i.e does not follow a normal distribution). [ref]
• T-Test same as the Mann Whitney but for normally distributed data, in other words use for comparing two means
• Chi Square test. used for statistical hypothesis testing for categorical data – is the data observed different from that predicted by the null hypothesis. Needs to use numerical values not percentages.Chi-square should not be calculated if the expected value in any category is less than 5 (eg in your two by two table is any of the 4 boxes are expected to have less than 5 patients in them then you should use an alternative test such as a fisher’s exact test) [ref]
• Two tailed test. Most hypothesis testing is “two tailed”, from what I can work out it means that the p-value given is non directional in a two tailed test though it seems somewhat more complicated than this [ref]

Results Section

Research Study Guidelines

Flow diagrams in studies are encouraged for both diagnostic and therapeutic studies. It makes it easier to see if the population was highly selected. EG we screened 10000 patients and included 57….

• Diagnostic studies
  • STARD guidelines on reporting diagnostic studies [25 part checklist]
  • QUADAS tool for diagnostic studies
• Randomised trials
  • CONSORT checklist [25 items]
• Systematic reviews
  • PRISMA
  • Cochrane handbook

Kaplan Meier Curve [ref]

• The length of time following randomisation until occurrence of a specific outcome is referred to as “time to event data” or “survival data.” The end point does not have to be death or even an adverse event
• this data is displayed in a Kaplan Meier curve
• hazard ratios can be used to compare and present such data
• if people don’t have an event within time of follow up the data are often described as right censored

What is a p value

• “the P value is the probability of obtaining the observed difference between treatment groups … if there was [in reality] no difference between treatment groups in the population, as specified by the null hypothesis.” [Sedgwick P. Understanding P values. BMJ (Clinical research ed). 2014;349:g4550.]
• interestingly p values do not indicate the direction of the difference you need to look at the  numbers to work that out
• p values indicate whether sample data supports a certain hypothesis. It is not able to say whether any hypothesis is true or false as this would require sampling an entire population.
• “the p value is the probability that the null hypothesis is true. The smaller the p value is, the less likely the null hypothesis is to be true” [Goodacre 2]
• Both p values and confidence intervals can tell you whether a result is statistically significant or not [ie p<0.05 or CI not crossing 1]
• Too many p values in an article suggest the possibility of multiple hypothesis testing and an increased risk of type I statistical errors
• “Statistical significance implies that the difference seen in the sample also exists in the population. Clinical significance implies that the difference between treatments in effectiveness is clinically important” [ref]

Confidence intervals

• in general viewed more positively
• The 95% confidence interval is a range of values around an estimate that have a 95% probability of encompassing the ‘‘true’’ value of that estimate. Put simply, the true value probably lies within the confidence interval. The confidence interval will tell you how precise an estimate is. The wider the confidence interval, the less precise is the estimate
• Both p values and confidence intervals can tell you whether a result is statistically significant or not [ie p<0.05 or CI not crossing 1]
• Confidence intervals provide information about the potential magnitude of an effect, regardless of whether or not the result is statistically significant; p values only tell you how statistically significant the result is
• Confidence intervals can be used to estimate the likelihood of a type II statistical error.  If important clinical differences exist within the range provided then a type II error may have occurred.

 Validity/Generalisability

• Validity = is this finding true?
• Generalisability = is this finding applicable elsewhere?

Internal/External Validity

• Internal validity is the extent to which the observed treatment effects can be ascribed to differences in treatment and not confounding, thereby allowing the inference of causality to be ascribed to the treatment
• external validity is the extend to which the results can be seen as generalisable to the population the study was meant to represent

Chance = random error = imprecision

Bias = systematic error [tend to produce results that are consistently wrong in the wrong direction] = inaccuracy

• eg Allocation bias is a systematic difference between participants in how they are allocated to treatment

Confounding is an error of interpretation – ie correlation and causation

Accuracy/Precision: See chance/bias

Efficacy: A study of efficacy determines whether a treatment can work under ideal conditions.

Effectiveness: A study of effectiveness shows whether a treatment actually does work under normal conditions

NNT:

• The NNT is the number of patients who would need to receive the treatment to avoid one negative outcome such as death. It is calculated as 1/ARR [absolute risk reduction]. eg in a 5% absolute risk reduction, the NNT = 1/0.05 = 20 (ie, 20 patients would need to be treated to avoid one death)

Odds Ratio:

• An odds ratio (OR) is a measure of association between an exposure and an outcome [ref]
  • NB this makes it less likely to come up in the exam as we’re more likely to get diagnostic or therapeutic studies not observational studies.
• A hazard ratio is used to compare time to event data (sometimes called survival data, see Kaplan Meier curves) [ref]
  • the main distinguishing point here is with relative risks which are cumulative over a study and the end point is only at the end of the study eg the probability of death at the end of the study can be used to calculate a relative risk. Hazard ratios measure time to event data where the outcome is instantaneous [ref]

Hawthorne Effect:

• the observation that people change their behaviour when they think that you are watching them. Therefore any intervention, if subsequently monitored, will produce a recordable change in processes or outcomes, which is lost when monitoring ceases

Interobserver error (reliability)

• Reliability cannot be estimated by simply measuring the percentage agreement between two observers because agreement may occur simply by chance
• The most common method for estimating reliability is to measure the kappa score
• A kappa is a measure of agreement between two observers in, for example, their diagnoses. It takes into account the amount of agreement that would have occurred simply by chance (as a result a kappa will be lower than simple measures of agreement).  It is not the proportion of observations for which they agreed. It is derived by comparing the overall observed and expected proportions of agreement between the observers. [ref]
• useful post describing difference between reliability and validity here

What is a receiver operator curve?

• basically a combination of sens/spec. The optimal cut-off score is a trade-off between sensitivity and specificity based on the implications of correctly identifying patients with  disease and incorrectly identifying controls as positive (false positives) [ref]
• The receiver operating characteristic curve therefore provides a graphical representation of the proportion of patients with disease correctly identified as positive against the proportion of control patients incorrectly identified
• the closer the receiver operating characteristic curve is to the upper left corner, the higher the overall accuracy of the screening test across all potential cut-off scores. For that reason, the cut-off score closest to the top left hand corner is typically chosen as the optimal cut-off score. However, this does assume that the implications of a false positive and a false negative result are similar.
• the number given is usually “area under” the ROC and is a broad description of overall accuracy of any given test
• lowest value = 0.5, highest value = 1
• here’s a recent EMJ paper discussion ROC curves.

Prevalence

•  The proportion of the population with the condition of interest

Sensitivity

• The proportion of patients with the disease who are correctly identified by the test. or…
•  probability that a test result will be positive when the disease is present (true positive rate).
• the actual calculation is: sensitivity = true positive/(true positive + false negative)
• NB independent of prevalence [though if 2 very different populations are actually studied you might get different sensitivities]

Specificity

• The proportion of patients without the disease who are correctly identified by the test. or…
• probability that a test result will be negative when the disease is not present (true negative rate)
• the actual calculation is: specificity = true negative/(true negative + false positive)
• NB independent of prevalence

PPV

• The proportion of patients in a population with a positive test who genuinely have the disease. or…
• probability that the disease is present when the test is positive
• the calculation PPV = true positive/(true positive + false positive)
• Though you need to know the prevalence of disease in that population to work it out. I think of it as somewhat similar to a post test probability (though I’m pretty sure they’re not actually the same. PPVs can be used for populations it seems whereas post test probabilities seem to only apply to individual patients)
• Positive predictive value increases when prevalence increases

NPV

• The proportion of patients in a population with a negative test who genuinely do not have the disease. or…
• probability that the disease is not present when the test is negative.
• the calculation NPV = true negative/(true negative + false neagtive)
• See notes above for PPV.
• Negative predictive value decreases when prevalence increases
• NB dependent on prevalence

Likelihood ratio

•  applies to a piece of diagnostic information, such as an observation, a clinical finding or a test result
• Likelihood ratio of positive test = sensitivity/(1-specificity)
• Likelihood ratio of negative test = (1-sensitivity)/specificity

Types of data (note different manners of presenting data and statistical tests are used for specific data types)

• Normally distributed data = data that normally occurs in typical normal distribution over a population (bell curves and all that). Eg BMI, normal body temperature etc…
• Skewed data = does not follow a normal distribution – note that most medical data in the studies we look at will be like this – length of stay a good example – there will always be crazy outliers.
• Continuous Data = Continuous Data can take any value (within a range)
• Categorical Data = a categorical variable is a variable that can take on one of a limited, and usually fixed, number of possible values, thus assigning each individual to a particular group or “category.”[ref]
• InterQuartile Range = the difference between the upper and lower quartiles, IQR = Q3 − Q1. [ref] The range formed by the quartile either side of the median is another way to describe it. The first quartile (Q1) is defined as the middle number between the smallest number and the median of the data set. The second quartile (Q2) is the median of the data. The third quartile (Q3) is the middle value between the median and the highest value of the data set. Note that the IQR is used to describe the spread of data around a median (ie in skewed data), standard deviation is used to describe the spread of data around a mean (ie in normally distributed data).
• Median = The median of a finite list of numbers can be found by arranging all the observations from lowest value to highest value and picking the middle one (e.g., the median of {3, 3, 5, 9, 11} is 5). If there is an even number of observations, then there is no single middle value; the median is then usually defined to be the mean of the two middle values (the median of {3, 5, 7, 9} is (5 + 7) / 2 = 6) [ref]
  • Why use it? When data is skewed (ie not normally distributed) then the median gives a better impression of the centre of the data and is less affected by extreme values
• Mean = this is the average of a set of values. More useful in normally distributed data sets.

—

Probably (hopefully) too advanced for the exam

• Parametric and non parametric tests
  • a bit to do with normally and non normally distributed data though sometimes it is appropriate to do parametric tests on non normally distributed data.
  • Regression, multivariate analysis and any kind of statistical modelling

Important References:

Steve Goodacre series [EMJ, sadly not FOAMed] I would consider these required reading

1. Concepts and definitions
2. Statistics
3. Evaluation of a therapy
4. Evaluation of service organisation 
5. Evaluation of a diagnostic test
6. Systematic reviews

Sedgwick Series [BMJ] [note CCR did this already][sadly no longer open access]

A full list can be found here

• Sample Size and Power [pdf]
• Absence of evidence not evidence of absence [pdf]
• Superiority Trials [pdf]
• Non Inferiority Trials [pdf]
• P Values [pdf]
• Type I and type II errors [pdf]
• What is a non randomised controlled trial [pdf]
• Clinical v statistical significance [pdf]
• Understanding statistical hypothesis testing [pdf]
• Open label trials [pdf]
• Crossover trial [pdf]
• Block Randomisation [pdf]
• Internal v external validity [pdf]
• Placebo controlled trials [pdf]
• Relative risk v odds ratio [pdf]
• Retrospective cohort studies [pdf]
• Case control studies [pdf]